Quadratic Gaussian Splatting: High Quality Surface Reconstruction with Second-order Geometric Primitives

摘要

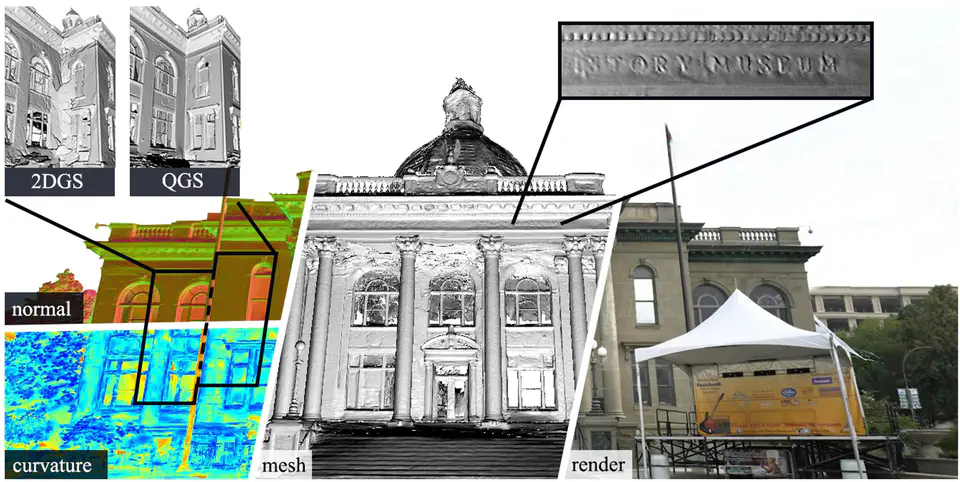
We propose Quadratic Gaussian Splatting (QGS), a novel representation that replaces static primitives with deformable quadric surfaces (e.g., ellipse, paraboloids) to capture intricate geometry. Unlike prior works that rely on Euclidean distance for primitive density modeling—a metric misaligned with surface geometry under deformation—QGS introduces geodesic distance-based density distributions. This innovation ensures that density weights adapt intrinsically to the primitive’s curvature, preserving consistency during shape changes (e.g., from planar disks to curved paraboloids). By solving geodesic distances in closed form on quadric surfaces, QGS enables surface-aware splatting, where a single primitive can represent complex curvature that previously required dozens of planar surfels, potentially reducing memory usage while maintaining real-time rendering via efficient ray-quadric intersection. Experiments on DTU, Tanks and Temples, and MipNeRF360 datasets demonstrate state-of-the-art surface reconstruction, with QGS reducing geometric error (chamfer distance) by 33% over 2DGS and 27% over GOF on the DTU dataset. Crucially, QGS retains competitive appearance quality, bridging the gap between geometric precision and visual fidelity for applications like robotics and immersive reality.